Hans Lugtigheid
Download Article : English / Nederlands
Abstract The v in the Lorentz transformation is the velocity of the origin of the second frame of reference. A point with no dimensions. From this v we cannot conclude a maximum speed (or anything) for physical objects. The c is the velocity of information. We can choose c to be any value and we see that that chosen value of c is measured the same in both reference frames. Then the speed of light is not a special case. The Lorentz transformation is an approximation of the Galileo transformation in which information has velocity c = ∞. The Galileo transformation is ‘real-time’. We thereby consider a (absolute) frame of reference from any point in the universe. We can not establish absence of movement and we do not have information traveling at infinite velocity. Therefore the Lorentz transformation is our best approximation of the Galileo transformation and thus of reality.
Introduction The measured invariance of the velocity of light leads to the Lorentz transformation. But what does the Lorentz transformation tell us about the invariance of the velocity of light? And what does the Lorentz transformation tell us about the maximum velocity in the universe? In this article we look at what we exactly can and cannot conclude from the parameters v and c in the Lorentz transformation. The v in the Lorentz transformation is the velocity of the origin of the second frame of reference. A point/location which has no dimension. We can not conclude a maximum velocity (or anything) for physical objects from this v. In the Lorentz transformation the velocity of light c is the velocity of information in the measurement. We can take any value c for the velocity of information. We find the chosen value of c for information to be the invariant value in the Lorentz transformation. Then the velocity of light is not a special case. When we take c = ∞ in the Lorentz transformation we get the The Galilean transformation. We investigate what it means when c → ∞ in the Lorentz transformations. We consider a (absolute) frame of reference with origin a point in the universe and the Galileo transformation as ‘real time’ distance and time. We can not establish or measure absence of movement and simultaneity. Therefore we look at the Lorentz transformation as an approximation of ‘real time’ distance and time as described by the Galileo transformation.
1. On the v in the γ in the Lorentz transformation
Let us take two reference frames with origins O and O’. The Lorentz transformation gives:

So the origin O’ moves away from O with velocity v. In the Lorentz transformation O’ is a point with no dimension. Furthermore, we only calculate with the location and velocity of the point O’. Hence a physical object (having positive dimension(s)) can travel alongside O’ with velocity v, but the v in the Lorentz equations is not the velocity of that physical object. From the above it follows that we cannot conclude anything about a physical object from the v in the γ in the Lorentz equations. In particular, we can not conclude that a physical object can not move faster than the velocity of light. Consequently, calculations and measurements with and, especially, conclusions based on the v in the Lorentz equations being the velocity of a fysical entity must be reviewed.
Hence, when a fysical entity moves with velocity s, we get:
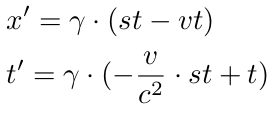
Because s is independent of v and c we can choose the value of s freely. Now take s > c. Then we see that there is no problem in the Lorentz equations.
2. On the c in the γ in the Lorentz transformation
In the derivation of the Lorentz transformation the velocity of light is used to measure distance and time from O’ to x and back (Einstein, 1905: ‘From the origin of system k let a ray be emitted ….’). Thus the velocity of light or c is the velocity of information (Cf. Ruan, 2018).
The velocity of information c is measured the same in both reference frames. Thus when x = ct then x’ = ct’. In the Lorentz equations we can take any positive value for the velocity of information c. We now take the velocity of information c small, say c = 10 mph. We can take v = 20 mph. (Remember: The origin O’ is a location from where we measure. This location O’ has no dimension, exists only in our minds, and can go at any velocity.)
Note that v > c leads to a negative value in the square root in γ. This doesn’t mean that nothing can go faster than 10 mph. It means that when a point O’ moves faster with velocity v than the velocity of information (c) then it is not possible to send information with speed c to the moving point O’.
Also when c = 10mph then this velocity is measured the same in both frames of reference, thus when x = 10mph.t then x’ = 10mph.t’. Note also that in this case the velocity of light is not measured the same in both frames of reference. Thus the velocity of information that we choose is the (only) velocity that is measured the same in both frames of reference.
Hence the Postulate: ‘The velocity of light is equal in both frames of reference’ (Einstein, 1905) is not correct. Accurate is: ‘When information has velocity c then that velocity c will be measured equal in both frames of reference’.
Now take c equal to the velocity of light. We cannot conclude from the Lorentz equations that nothing can go faster than the velocity of light. For if we could then we would conclude likewise from the Lorentz equations that nothing can go faster than 10mph when c = 10mph. We can only conclude that we cannot send a message with velocity c to the point O’ that moves at velocity v > c.
So the velocity of light is not different from other velocities. And we can not conclude anything unique or special for the velocity of light from the Lorentz transformation. Many measurements and calculations will be in accordance with the Lorentz equations. However, the fact that those measurements and calculations are in accordance with the Lorentz equations does not prove that the velocity of light is the maximum velocity in the universe nor that the measured equality of the velocity of light in both frames of reference is unique for the velocity of light.
3. Lorentz- and Galileo transformation
When c → ∞ then we get the Galileo transformation:

Let the velocity of information c equal ∞. Then with the Galileo transformation we measure everything, including the origin of the moving frame of reference and locations, ‘as is’ at the same time. With velocity of information c = ∞ we can then also measure simultaneity.
We can not measure with information at infinite velocity. Nothing that we know goes that fast. But everything ‘as is’ is the reality and the Galileo transformation describes the absolute coordinates with respect to both frames of reference. The Lorentz transformation is an approximation of the Galileo transformation. When c gets larger, and eventually gets closer to ∞ and v << c then the approximation gets better. When v approaches c it takes a very long time to send information with velocity c to a point O’ that is moving at velocity v. In that case the approximation gets worse.
Still, the prediction of the values according to the Lorentz transformation is equal to the measurement and both are real. But that does not mean that those values describe ‘realtime’ values. They are (bad) approximations of the ‘realtime’ values of the Galileo transformation. When v = c the approximation is off limits because then we can not send information with speed c to a point O’ that is moving at velocity v= c. And thus we can not measure distance to O’. We get t’ = ∞ meaning that it will take information forever to travel to O’.
This approximation also applies with respect to adding velocities:
When c → ∞ then
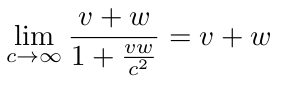
When according to the addition of velocities v and w are always < c and c → ∞ then v and w can be any velocity < ∞. In this the velocities v and w are the velocities of the respective origins of two reference frames. Points with no dimension. When we deal with velocities of physical objects, say r and s we get for addition of velocities according to the Lorentz transformation:
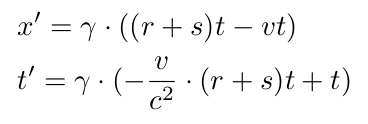
And, with c → ∞, we get for addition of velocities according to the Galileo transformation:
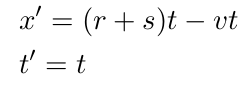
Note that in the Lorentz transformation in the first frame of reference with origin O distance (x) and time (t) are measured with infinite velocity (∞), while in the second frame of reference with origin O’ distance (x’) and time (t’) are measured with the velocity of light/information (c).
4. Absence of movement and absolute frames of reference
Space is infinite. Therefore every point in space can function as the origin O⁰ of a frame of reference. Points in space do not move. Therefore the frame of reference with origin O⁰ is an absolute reference frame. The origins O and O’ of the frames of reference in the Lorentz transformation have absolute distances to O⁰, as decribed with the Galileo transformation.
We cannot establish absence of movement. Thus we cannot ‘fixate/measure’ the origin O⁰ of and distances from that absolute frame of reference. The Lorentz transformation gives us an approximation of reality to measure distance and time. We always have to keep in mind that this is an approximation of the Galileo transformation. With information traveling at the velocity of light this is the best approximation we can get.
When we take the point O⁰ as origin of the first frame of reference and our location (‘earth’) as origin of the second frame of reference then we are moving with velocity v away from O⁰. Note that we cannot know the absolute velocity v. Hence every measurement we take is an approximation of reality. And we can not determine how close this approximation is because we don’t know the value of v.
Conclusion
From the parameters v and c in the Lorentz transformation we can not conclude that the velocity of light is the maximum velocity in the universe. We have to review measurements and calculations with the v in the Lorentz transformation being the velocity of a physical entity and conclusions based on these measurements and calculations.
When information has velocity c then that velocity c will be measured equal in both frames of reference. This is not unique for the velocity of light. The Lorentz transformation is an approximation of the Galileo transformation. The approximation gets better when c gets larger (with v << c) and ultimately c → ∞. When v → c the approximation gets worse.
Prediction and measurement of values according to the Lorentz transformation are equal. This equality might suggest accuracy and thus validity. But prediction and measurement are still approximations of values according to the Galileo tranformation and become, when v → c, meaningless.
Hence the relevant limit in the Lorentz transformation is lim c → ∞.
Every point in space can function as the origin O⁰ of an absolute frame of reference. The Galileo transformation gives the real time and location coordinates. We can not determine absolute movement and/or rest. Therefore we only have measurements that are uncertain approximations of absolute values. This is a fundamental uncertainty.
When we work with the Lorentz equations we have to be very carefull about what moves at which velocity and which parameter (v, c or none) we assign to what. Einstein could not explain the invariance of the velocity of light. He therefore took it as a postulate and derived the Lorentz transformation from that. Looking at the Lorentz transformation we see that the invariance of the velocity of light is explained by it being the velocity of information of the measurement. If we take a different velocity of information we get that different velocity as invariant velocity. This explains the invariance of the velocity of light by using Newtonian physics and takes out the presumed mystery.
With the above results we can ask old and new questions, and get new answers and ideas about how we see space, time and the universe. Also the question arises whether we still have two different theories that need unification. I leave it to the reader to explore this further.
See also: Lorentz transformation – a conversation
References:
A. Einstein, On the electrodynamics of moving bodies, Ann. Phys. (Berlin)} 1905, vol. 322, p. 891-921
X. Ruan, The Role of Light in Observation: Why is the Speed of Light Invariant?, www.vixra.org/abs/1807.0267 2018
![]()
This work is licensed under a
Creative Commons Attribution 4.0 International License.