On the square root in the $gamma$ in the Lorentz transformation -

On the square root in the Lorentz transformation

Introduction

In the formulas of the Lorentz transformation there is a square root in the $\gamma$ .

$x' = \gamma (x-vt)$

$t' = \gamma (- \frac{vx}{c^{2}} +t)$

$\gamma = \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$

The derivation of the formulas is based on an echo-measurement. A signal with speed c goes forward and at x switches direction and returns with speed c in the opposite direction to meet the origin O’ which moves at speed v along the same axis. We look at the (basic) echo-measurement.

When we derive formula’s we will see that, depending on the relative value of v and c, a square root equal to the one in $\gamma$ appears in the equation. The echo measurement is a minimal and sufficient condition for this square root.

Echo measurement

We consider two cases:
Case 1: v > 0 and
Case 2: v < 0.

Case 1: v > 0

First we look at v > 0. Wed then have two possibilities: v < c and v > c.

First possibility : v < c.
This is the basis setup of a echo-measurement. See figure 1.

This is the basic situation for an echo-measurement. From the origin O a signal goes with speed c to x and returns to meet O’. O’ moves forward with speed v. The signal and O’ meet in point y.

Second possibility : v > c. See figure 2.

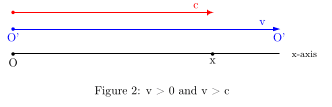
Now v > c. So we see that the signal with speed c and O’ never meet – O’ goes faster than c.

Hence there is no echo-measurement possible. The fact that there is no measurement possible should be reflected in the derived formulas. So there must be a term in the formula that signals that there is no measurement.

So there is a problem when v > c, or c – v < 0. A likely term to show the impossibility of a measurement then is $\sqrt{c-v}$ . The square root of a negative number has no real value. Then the formula ‘protests’ when there is no measurement possible.

Case 2: v < 0

First possibility : |v| < c see figure 3.

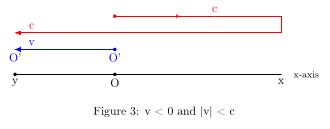
In this case the signal and O’ meet at y. Note that y is left from the original starting point.

Second possibility : c < |v|. See figure 4.

Now |v| > c. So we see that the signal with speed c and O’ never meet – O’ goes faster (to the left) than c.

Again there is no echo-measurement possible. The fact that there is no measurement possible should be reflected in the derived formulas. So there must be a term in the formulas that signals that there is no measurement.

So there is a problem when |v| > c, or – v > c or c + v < 0. A likely term to show the impossibility of a measurement then is $\sqrt{c+v}$ . The square root of a negative number has no real value. Then the formula ‘protests’ when there is no measurement possible.

Discussion

From the above we see that in a formula for an echo-measurement the formula should result in a non-valid outcome when |v| > c. We have two logical signals: $\sqrt{c-v}$ and $\sqrt{c+v}$ .

When we combine these signals in a formula we get:

$\sqrt{(c+v)} * \sqrt{(c-v)} = \sqrt{(c+v) * (c-v)} = \sqrt{c^{2}-v^{2}}$

$= \sqrt{\frac{1}{c^{2}} * (1-\frac{v^{2}}{c^{2}})}$

$= \frac{1}{c} * \sqrt{1-\frac{v^{2}}{c^{2}}}$

We see that the term

$\sqrt{1-\frac{v^{2}}{c^{2}}}$

in the Lorentz transformations

${\gamma = \frac{1}{ \sqrt{1-\frac{v^{2}}{c^{2}}}}}$

comes as a result of the situations that there is no measurement possible. In those cases |v| > c.

In the above it is not necessary that c equals the speed of light.
Hence one has to be cautious to attribute the term in the square root in the $\gamma$ to another reason than that a measurement is not possible.

In addition consider that the v in the Lorentz transformations is the velocity of the point from which we measure, a point that has no physical dimensions.

Then this is leads to caution in using the $\gamma$ in the Lorentz transformations to conclude that nothing can go faster than the speed of light. There might just not be the possibility of a measurement when |v| > c.